北理工團隊在非晶體系結(jié)構(gòu)與動力學關(guān)聯(lián)上取得重要研究進展
發(fā)布日期:2022-06-30 供稿:物理學院 攝影:物理學院
編輯:王莉蓉 審核:姜艷 閱讀次數(shù):
近日,北京理工大學物理學院李艷偉研究員、姚裕貴教授同新加坡南洋理工大學數(shù)學物理學院Massimo Pica Ciamarra教授合作,在非晶體系結(jié)構(gòu)與動力學關(guān)聯(lián)問題上取得重要進展。提出塑性關(guān)聯(lián)長度可用于預(yù)測較長時間尺度下非晶體系的復雜動力學行為,如動力學變慢及動力學異質(zhì)性。該研究創(chuàng)新性的建立了塑性與動力學的關(guān)聯(lián),為非晶玻璃化轉(zhuǎn)變這一公認學術(shù)難題提供了新的思路。該研究工作發(fā)表在物理學頂尖期刊Physical Review Letters上。
液體降溫過程中,可能會在低于結(jié)晶溫度時不結(jié)晶,形成過冷液體,進一步降溫,過冷液體會經(jīng)歷玻璃化轉(zhuǎn)變形成非晶固體。玻璃化轉(zhuǎn)變機制是統(tǒng)計物理,軟物質(zhì)物理,高分子物理等領(lǐng)域中的公認難題。液體-非晶固體轉(zhuǎn)變過程中,體系黏度可有近14個量級的攀升,而其靜態(tài)結(jié)構(gòu)卻變化不大,保持長程無序的狀態(tài),這與液體-晶體轉(zhuǎn)變截然不同。此外,在非晶液-固轉(zhuǎn)變過程中,體系的動力學會越來越慢,動力學關(guān)聯(lián)函數(shù)呈現(xiàn)兩步松弛,并伴隨體系不同區(qū)域粒子運動快慢不同等復雜而有趣的現(xiàn)象。玻璃體系動力學與體系結(jié)構(gòu)有沒有關(guān)系,如果有關(guān)系,是什么樣的結(jié)構(gòu)性質(zhì)決定體系的動力學的?圍繞這一問題,文獻中報道了諸如基于局部彈性性質(zhì)與動力學的關(guān)聯(lián),如通過描述粒子振動強度的Debye-Waller因子,或其簡諧近似下的均方位移,或低頻振動模的參與分數(shù)來預(yù)測體系中的快慢粒子。然而這些彈性性質(zhì)在較短時間與動力學有對應(yīng)關(guān)系,而在較長時間尺度,如弛豫時間的尺度,與動力學關(guān)聯(lián)較弱。尋求新的視角理解玻璃化轉(zhuǎn)變中結(jié)構(gòu)與動力學的關(guān)聯(lián)顯得尤為重要。
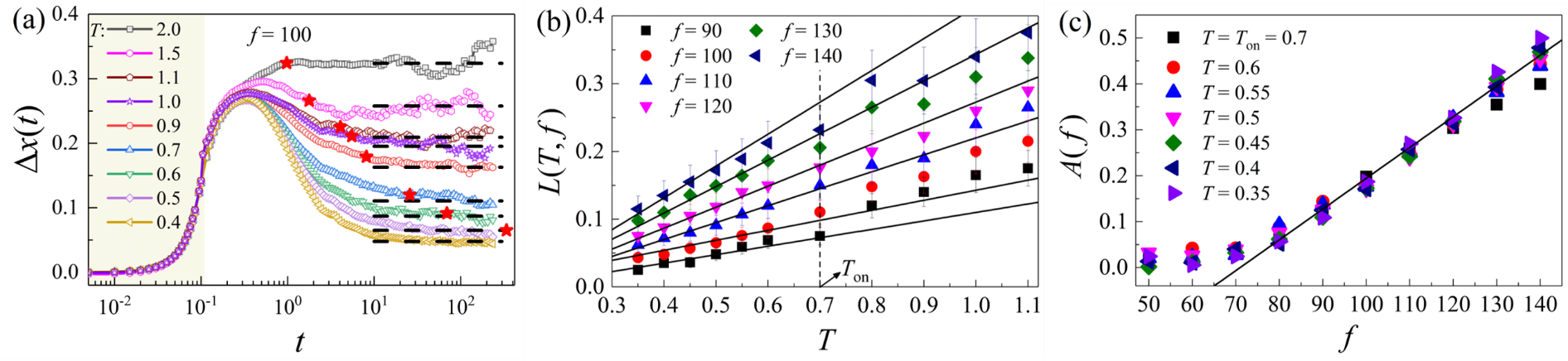
圖1 (a) 對粒子施加一外力,其大小f = 100時 (陰影區(qū)時間間隔內(nèi)),粒子平均位移隨時間的變化,黑色虛線表示較長時間下平均位移趨近一平臺值,即不可逆位移L(T, f)。(b) 不同外力大小時,不可逆位移L(T, f)隨溫度的依賴規(guī)律。
團隊設(shè)計了新的探測玻璃體系靜態(tài)結(jié)構(gòu)的手段,具體為,在短時間內(nèi),對粒子施加一固定大小,方向隨機選取的力,觀察撤去力之后,粒子不能回彈的位移,即不可逆位移有多大。圖1(a)展示了當對粒子在0.1(約化單位)時間間隔內(nèi)施加一外力大小為f = 100(約化單位)的力時,粒子平均位移隨時間的演化規(guī)律。較長時間下,此平均位移趨近一平臺值,即黑色虛線標出的不可逆位移L(T, f),顯然,溫度越低,不可逆位移L(T, f)越小。近一步的研究發(fā)現(xiàn),L(T, f)正比于 T - T 0 (圖1 (b)),其中 T 0為Vogel–Fulcher–Tammann (VFT) 方程預(yù)測的非晶體系的理想玻璃化轉(zhuǎn)變點,因此,L(T, f)在理想玻璃化轉(zhuǎn)變點外推為0。進一步分離變量,我們可得到L(T, f) = ξ(T)A(f), 其中塑性長度ξ(T)∝( T - T 0 ), A(f) ∝( f - f 0)。塑性長度ξ(T)與體系弛豫時間存在指數(shù)依賴關(guān)系(圖2),因此建立了塑性長度與非晶體系慢動力學的聯(lián)系。
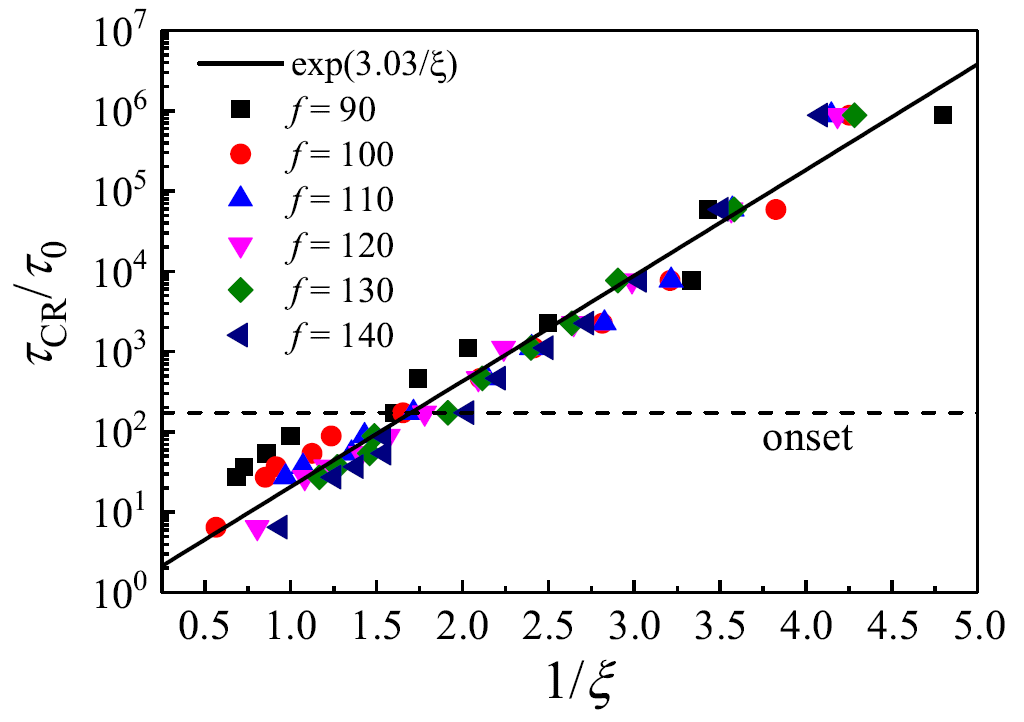
圖2 體系弛豫時間與塑性關(guān)聯(lián)長度的依賴關(guān)系。
為了探索塑性長度與體系動力學異質(zhì)性之間的關(guān)聯(lián),計算了每個粒子的同構(gòu)型(iso-configurational ensemble)系綜下的平均均方位移<? r 2CR( t )>iso,并通過Spearman等級相關(guān)系數(shù)定量表征了動力學參數(shù)<? r 2CR( t )>iso與靜態(tài)參數(shù)的關(guān)聯(lián)。為了對比,靜態(tài)參數(shù)除了我們提出的塑性長度外,還包含三個常見的通過彈性性質(zhì)定義的量,包括Debye-Waller因子< u 2>,其簡諧近似下的均方位移ψ,以及低頻振動模的參與分數(shù)p。結(jié)果表明,彈性性質(zhì)的相關(guān)量僅在較小的振動尺度與動力學存在關(guān)聯(lián),而塑性長度在弛豫時間或更長時間尺度與動力學存在關(guān)聯(lián) (圖3)。這展現(xiàn)出塑性長度可能是與體系弛豫行為更相關(guān)的一個靜態(tài)量。為玻璃化轉(zhuǎn)變結(jié)構(gòu)與動力學關(guān)聯(lián)問題探索了一個新思路。
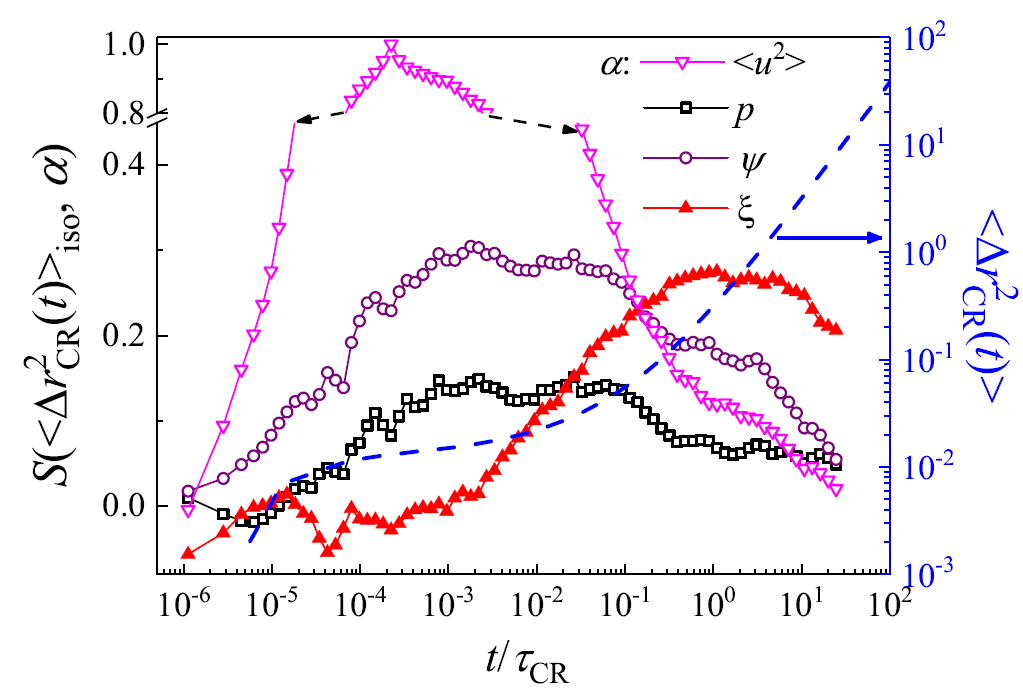
圖3 不同的靜態(tài)量包括Debye-Waller因子< u 2>,其簡諧近似下的均方位移ψ,低頻振動模的參與分數(shù)p,以及塑性長度ξ與動態(tài)量<<?r2CR(t)>>的Spearman等級相關(guān)系數(shù)S。
相關(guān)工作發(fā)表在Physical Review Letters上,北京理工大學物理學院李艷偉研究員為第一作者兼通訊作者,北京理工大學物理學院姚裕貴教授和新加坡南洋理工大學Massimo Pica Ciamarra為論文共同通訊作者。該工作第一單位為北京理工大學物理學院,并得到國家自然科學基金、北京理工大學青年學者學術(shù)啟動計劃等項目的支持。
分享到:
