北理工教師在不可壓縮歐拉方程螺旋對稱解的集中性問題方面取得研究成果
發(fā)布日期：2023-06-07 供稿：數(shù)學與統(tǒng)計學院 攝影：數(shù)學與統(tǒng)計學院
編輯：王歡 審核：張希承 閱讀次數(shù)：
日前,，北京理工大學數(shù)學與統(tǒng)計學院萬捷副研究員在國際學術(shù)期刊《Mathematische Annalen》發(fā)表題為“Structure of Green’s function of elliptic equations and helical vortex patches for 3D incompressible Euler equations”的研究論文,。該論文給出了散度型二階橢圓算子Green函數(shù)的展開公式，并由此證明了無限管道區(qū)域上三維不可壓縮歐拉方程集中到渦絲方程的螺旋對稱渦補丁解的存在性和軌道穩(wěn)定性,。某種程度上給出了渦絲猜想在螺旋對稱情形下的一個證明,。
三維不可壓縮歐拉方程的渦絲猜想是流體力學中十分重要的問題之一。1908年,，DaRios和Levi-Civita通過研究截面半徑很小的渦管的運動,，得到渦管的中心線Γ滿足如下渦絲方程 ?tΓ="c?sΓ×?ssΓ,。該方程又稱為副法向曲率流(Binormal" Curvature Flow),。當三維不可壓縮歐拉方程的初始渦度場集中到一維曲線Γ(0)時，任意t時刻演化的渦度場是否會集中到滿足渦絲方程的Γ(t),，目前為止仍未解決,。該問題又稱為渦絲猜想，并受到了Davila,，F(xiàn)raenkel,，Jerrard， VanSchaftingen, Wei等著名數(shù)學家的廣泛關(guān)注,。目前這方面的研究主要針對幾種特殊情況：渦絲為直線,，平移圓周以及平移旋轉(zhuǎn)螺旋線。當渦絲是螺旋線時,，是否可以構(gòu)造一族三維歐拉方程的真實解,，使得對應(yīng)的渦度場的截面具有緊支集且集中到滿足渦絲方程的平移旋轉(zhuǎn)螺線，仍然是未知的,。其主要困難是求一類散度型半線性二階橢圓方程組解的集中性問題,，而散度型橢圓算子對應(yīng)Green函數(shù)的漸近展開是沒有的。
萬捷與中科院數(shù)學與系統(tǒng)科學研究院曹道民研究員利用橢圓方程理論,，創(chuàng)造性的給出散度型二階橢圓算子L=-??(K(x)?)在Dirichlet邊界條件下的Green函數(shù)的展開公式：
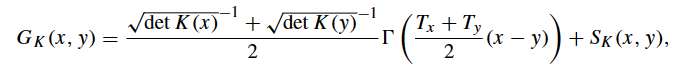
結(jié)合該式以及重排函數(shù)理論,，萬捷等人證明了存在一族三維歐拉方程的渦補丁解，使得對應(yīng)的渦度場Wε拓撲上為截面半徑ε的螺旋渦管，且當ε趨于零時Wε集中到滿足渦絲方程的平移旋轉(zhuǎn)螺線,。 利用能量,、角動量守恒以及緊性分析，文章還得到了渦補丁解在Lp擾動下的軌道穩(wěn)定性,?！禡athematische Annalen》期刊的審稿人評價“It's a solid work, with a significant contribution to an interesting problem and clever use of a broad set of techniques.”
這項研究工作是由萬捷副研究員與中科院數(shù)學與系統(tǒng)科學研究院曹道民研究員合作完成，萬捷副研究員為通訊作者,，本項工作得到國家自然科學基金和北京理工大學青年教師學術(shù)啟動計劃的資助,。
論文鏈接：https://link.springer.com/article/10.1007/s00208-023-02589-8
附個人簡介：
萬捷，特聘副研究員,，北理工數(shù)學與統(tǒng)計學院偏微分方程團隊成員,。本科畢業(yè)于中國科學技術(shù)大學、博士畢業(yè)于中科院數(shù)學與系統(tǒng)科學研究院,。長期從事流體力學特別是不可壓縮歐拉方程的研究工作,。在Mathematische Annalen 、Journal of Functional Analysis,、SIAMJournal Math Analysis 等權(quán)威期刊發(fā)表了十余篇高水平學術(shù)論文,。
分享到：