北理工朱蓉禪副教授在《The annals of Probability》上發(fā)表?_3^4動力模型格點逼近的研究成果
發(fā)布日期：2018-11-19 供稿：數(shù)學與統(tǒng)計學院
編輯：吳一凡 審核：田玉斌 閱讀次數(shù)：
日前，北京理工大學數(shù)學與統(tǒng)計學院朱蓉禪副教授在國際頂級學術(shù)期刊《The annals of Probability》上發(fā)表了題為《Lattice approximation to the dynamical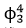 
model》的研究論文。該研究構(gòu)造了以格點上
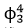場的逼近測度為不變分布的有限維系統(tǒng)收斂到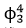動力模型。 這對應(yīng)于量子場論中重要的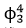場格點逼近，由此可以得到
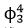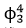動力模型以場為不變測度。
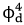動力模型是對量子場論中基本模型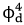場提出的隨機量子化模型，即構(gòu)造一個隨機偏微分方程即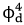動力模型使得當時間趨于無窮時方程的解依分布收斂到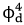場。由此運用隨機分析的方法研究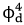場。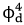動力模型是一類帶有奇異噪聲的隨機偏微分方程，如何在d="3時給出方程解的適定性是公開了很多年的問題。2011年英國帝國理工大學的Hairer教授在中用粗糙路徑理論處理方程解在一維空間的奇異性,并以此構(gòu)造了一維KPZ方程的解。之后，Hairer教授結(jié)合泰勒展開的思想提出了一套新理論：正則結(jié)構(gòu)理論(regularity" structure)，給出了次臨界條件下證明帶有奇異噪聲的隨機偏微分方程局部適定性的一般方法，這是隨機偏微分方程領(lǐng)域的重大發(fā)展。由此證明了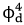動力模型局部適定性。Haire教授因此獲得了2014年Fields獎。同時，Gubinelli-Imkeller-Perkowski基于被控制的粗糙路徑(controlled rough path)和調(diào)和分析中的仿積提出了擬控制分布(paracontrolled distribution)的方法。這個方法也可以用來研究奇異的隨機偏微分方程。Gubinelli教授也因此受邀在2018年國際數(shù)學家大會作45分鐘報告。目前，這兩套方法是隨機分析領(lǐng)域的重大發(fā)展。
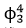場的格點逼近是研究和構(gòu)造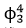場的一種重要方法，它保持了測度的鐵磁本質(zhì)和Osterwalder–Schrader公理。朱蓉禪副教授在上訴論文中運用擬控制分布首先研究了以格點上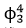場的逼近測度為不變分布的有限維系統(tǒng)。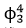動力模型可以看成是三維環(huán)面上的模型，因此要證明收斂性需要將格點系統(tǒng)模型延拓到環(huán)面上進行比較。這時延拓時會產(chǎn)生有限維投影算子，這個算子會導(dǎo)致擬控制分布中非常本質(zhì)的交換子估計不成立，分析方法無法運用。這時朱蓉禪副教授及合作者在論文中將投影算子中余項部分運用概率計算的方法證明了收斂。
這一結(jié)果進一步增進了人們對于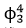場動力系統(tǒng)及其格點逼近之間的關(guān)系。既可以用來聯(lián)系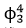場和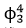動力模型，也可以用來構(gòu)造與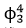場對應(yīng)的狄氏型，由此回答了以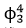場為參考測度的二次型可閉的公開問題。
該研究工作由朱蓉禪副教授和北京交通大學朱湘禪副教授合作完成。朱蓉禪副教授為本文的第一作者。本工作得到國家自然科學基金的支持。
論文鏈接地址：https://projecteuclid.org/euclid.aop/1517821226
【課題組及負責人簡介】
北京理工大學數(shù)學與統(tǒng)計學院概率團隊積極開展實質(zhì)性國際合作研究，團隊成員積極開展國際學術(shù)交流。
朱蓉禪，副教授，碩士生導(dǎo)師，本科畢業(yè)于四川大學、博士是中科院數(shù)學與系統(tǒng)科學研究院與德國比勒菲爾德大學聯(lián)合培養(yǎng)。德國比勒菲爾德大學訪問學者。長期從事隨機偏微分方程、狄氏型、隨機分析的研究工作，先后主持/完成了國家自然科學基金面上項目、青年項目。以第一/通訊作者在The annals of probability、Communication in mathematical physics、Journal of functional analysis、Journal of differential equaitons等期刊發(fā)表SCI論文20余篇。
分享到：