北理工取得AED誤差估計,、Eikonal方程正則性和全局結構相關研究成果
發(fā)布日期：2020-05-15 供稿：數(shù)學與統(tǒng)計學院
編輯：陶思遠 審核：田玉斌 閱讀次數(shù)：
日前，北京理工大學數(shù)學與統(tǒng)計學院溫海瑞老師與合作者在國際頂級學術期刊《Math.Comp.》及《Arch. Ration. Mech. Anal.》上發(fā)表題為 “Error estimates for the AEDG method to one-dimensional linear convection-diffusion equations”及題為 “Global structure and regularity of solutions to Eikonal equation”的研究論文,。
Hamilton-Jacobi（HJ）方程首先在經典力學中提出,，其在動態(tài)規(guī)劃、變分計算及最優(yōu)控制等方面都有廣泛而深刻的應用,。該類方程的數(shù)值模擬和理論分析工作一直是研究熱點,。數(shù)值計算方面，設計守恒,、相容和高精度的數(shù)值方法是人們關注的焦點,。理論分析方面，對于具有超線性,、嚴格凸Hamiltonian的方程的粘性解的性質研究相對完善,，但對于有幾何Hamiltonian的HJ方程的理論分析幾乎沒有。
AEDG方法由Iowa State Univ. Prof. Liu Hailiang及博士后M. Pollack首次提出,。該方法無需數(shù)值流通量,，并且是相容和守恒的。對線性對流擴散方程,，AEDG的穩(wěn)定性在CFL型條件下被證明,。
在此基礎上,溫海瑞老師和Prof.Liu Hailiang創(chuàng)造性的引進了兩個逼近空間、相應的雙線性算子和耦合的全局投影,，克服了交替發(fā)展系統(tǒng)中的多項式重合帶來的困難,，并重新設計了經典有限元誤差估計中經常用到的對偶方法，從而成功的從半離散AEDG格式的能量誤差提升到最優(yōu)的平方誤差,。對于空間離散,，利用任意高階多項式，設計了利用二階Crank-Nicolson及三階Runge-Kutta時間離散的全離散格式,，同時,，在CFL型穩(wěn)定性條件下,，得到了相應的最優(yōu)平方誤差階。
除HJ方程之外,，AEDG方法在守恒律,，對流擴散方程計算中都取得了很好逼近效果。其無需數(shù)值流通量的特性,，克服了一般DG方法中設計穩(wěn)定的流通量的困難,，文章的結果和新證明方法奠定了AEDG方法收斂性的理論基礎，具有重要意義,。
在HJ方程正則性理論方面,，對 Eikonal方程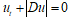
，由于對奇異點限制更弱,，在奇異點之外并不一定和初值具有相同的正則性等特性導致情況極其復雜。 同時,，其非光滑,、非嚴格凸的Hamiltonian為理論分析也帶來了巨大的挑戰(zhàn)。
溫海瑞老師及合作者利用次微分定義了不可微點處的特征線,，同時,，創(chuàng)造性的引入了有效特征及特征終止時間，對于C1和C2初值,，給出了奇異點集合的定義,、連通分支的可數(shù)性，給出了奇異點集合之外解的正則性及全局結構,。 審稿人評價該結果彌補了這類特殊HJ方程解的性質分析的理論空白,。
論文鏈接：
https://www.ams.org/journals/mcom/2018-87-309/S0025-5718-2017-03226-9/home.html
https://www.esaim-m2an.org/articles/m2an/abs/2018/05/m2an170163/m2an170163.html
https://link.springer.com/article/10.1007/s00205-018-01339-4
附個人簡介：
溫海瑞，講師,， 中國科學院數(shù)學與系統(tǒng)科學研究院獲得博士學位,，清華大學周培源應用數(shù)學中心博士后。從事Hamilton-Jacobi方程正則性,，守恒律大時間步長方法,，DG及保結構DG方法理論分析及數(shù)值模擬研究工作， 已在 Arch. Ration. Mech. Anal. , Math.Comp. 等本領域權威國際期刊上發(fā)表論文九篇,。
分享到：