北理工在界面反射研究中取得重要進(jìn)展
發(fā)布日期:2020-09-09 供稿:物理學(xué)院
編輯:周格羽 審核:姚裕貴 閱讀次數(shù):
日前,北京理工大學(xué)姚裕貴教授團(tuán)隊(duì)成員余智明及其合作者,在界面反射研究中取得重要進(jìn)展,發(fā)現(xiàn)界面反射中反常位移環(huán)流可以是量子化的,為物理學(xué)中重要但非常罕見的量子化的物理量增添了新的一員。
界面反射是一個(gè)普遍存在且早已為人們所熟知的物理過程,但該領(lǐng)域的研究依然在蓬勃發(fā)展。在界面反射中,一個(gè)有意思的物理現(xiàn)象是所謂的反常位移現(xiàn)象,指的是,當(dāng)粒子在界面處發(fā)生散射時(shí),其出射點(diǎn)和入射點(diǎn)在界面上是分開的,存在一個(gè)位移差。反常位移現(xiàn)象最早是在光學(xué)中發(fā)現(xiàn)的,而后由于電子光學(xué)研究的興起,該現(xiàn)象也被引入到電子體系當(dāng)中,甚至在金屬超導(dǎo)界面的Andreev反射中也被發(fā)現(xiàn)了。因此,反常位移是一個(gè)普遍存在的物理現(xiàn)象,研究和揭示新奇的反常位移行為不僅是一個(gè)基本的物理研究問題,也可以為探測(cè)材料物性提供一個(gè)新的潛在手段。
近幾年,余智明、姚裕貴教授和楊聲遠(yuǎn)教授等人合作在反常位移研究領(lǐng)域取得了一系列重要進(jìn)展。在2017年,余智明等人首次指出在金屬和s-波超導(dǎo)界面處的Andreev反射中可以存在橫向位移[Physical Review B, 96,121101 (2017)],并其后在2018年,發(fā)現(xiàn)非傳統(tǒng)超導(dǎo)可以獨(dú)立得導(dǎo)致反常橫向位移的產(chǎn)生,而不需要體系具有自旋軌道耦合,極大得拓展了反常橫向位移的存在條件[Physical Review Letters 121, 176602 (2018)]。上述工作為余智明等人在近期發(fā)現(xiàn)量子化的反常位移環(huán)流奠定了非常重要的研究基礎(chǔ)。
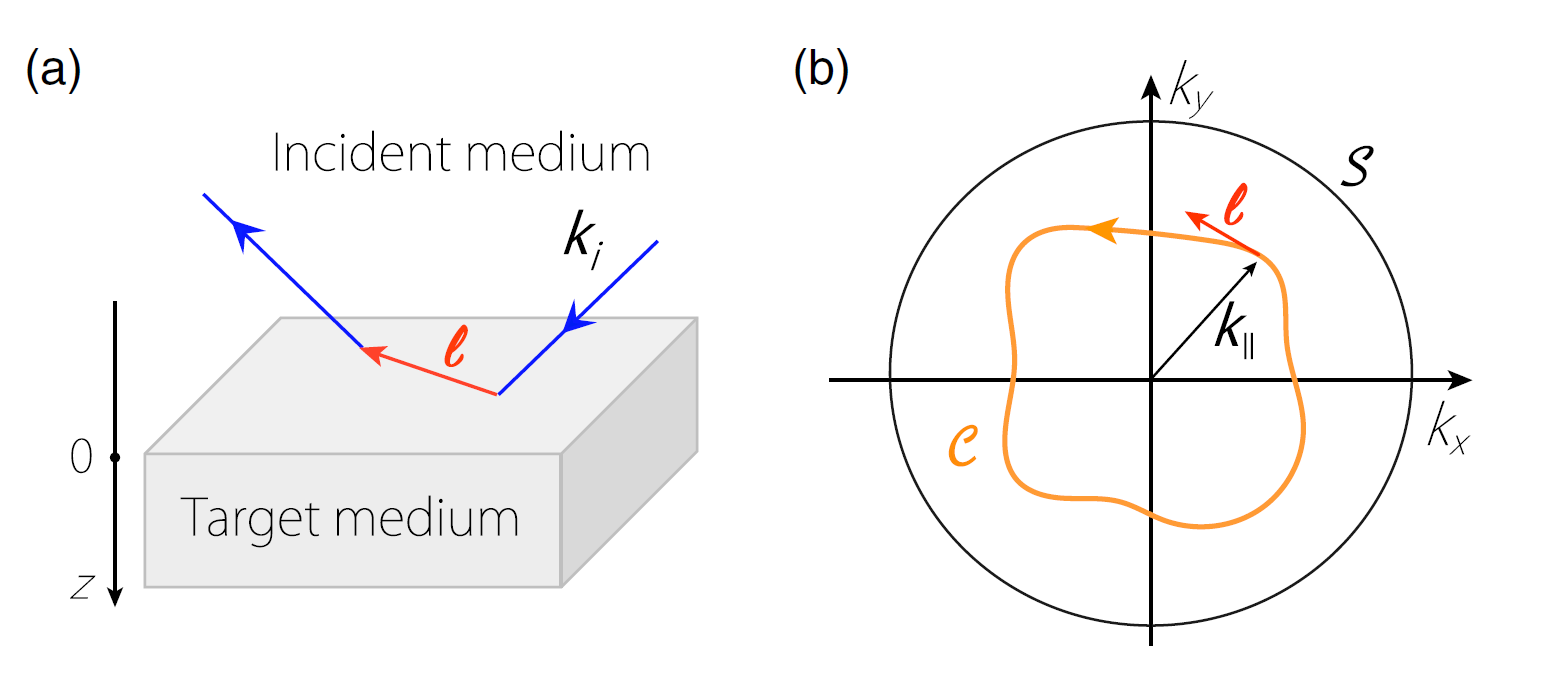
圖1:(a)界面反射中反常位移的示意圖。藍(lán)色線段表示入射和反射的電子流,紅色線段代表反常位移。(b)反常位移是隨界面動(dòng)量變化的一個(gè)矢量。C代表反常位移在界面動(dòng)量空間中的環(huán)路積分。
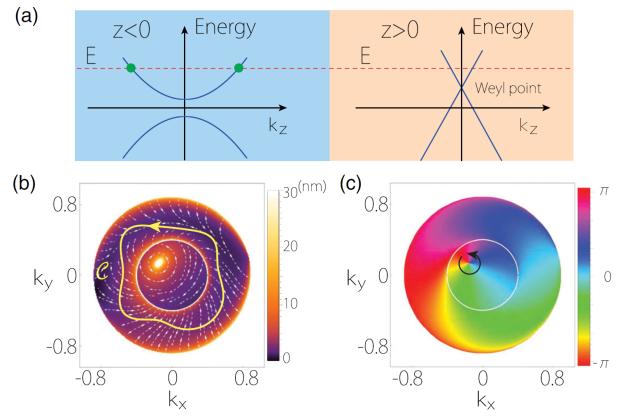
圖2:(a)普通金屬和外爾半金屬所構(gòu)成的模型示意圖。(b)反常位移在界面動(dòng)量空間的矢量場(chǎng)。箭頭代表矢量的方向,顏色代表矢量的絕對(duì)值。(c)反射振幅的相位隨界面動(dòng)量的變化。
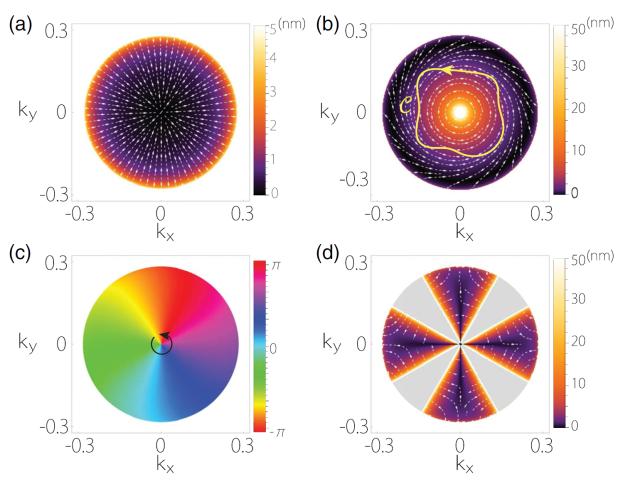
圖3:Andreev反射中的反常位移在(a)s-波超導(dǎo),(b)手性p-波和(d)d-波超導(dǎo)下的行為。(c)手性p-波情況下,Andreev反射振幅的相位角在界面動(dòng)量空間下的行為。
研究反常位移現(xiàn)象的一般性模型可分為兩部分,一為入射區(qū)域,二為透射或目標(biāo)區(qū)域,如圖1(a)所示。當(dāng)入射的粒子束(比如光或電子)從入射區(qū)域向目標(biāo)區(qū)域運(yùn)動(dòng)時(shí),其在界面反射時(shí)可以產(chǎn)生反常位移現(xiàn)象。反常位移是一個(gè)定義于界面動(dòng)量空間的矢量,其定義范圍為入射區(qū)域費(fèi)米面在界面動(dòng)量空間上的投影,如圖1(b)所示。余智明等人首先通過對(duì)稱性分析,指出當(dāng)入射區(qū)域具有某些特定的對(duì)稱性,反常位移的環(huán)流必然是量子化的。特別重要的是,該量子化的對(duì)稱性要求其實(shí)并不苛刻。許多實(shí)驗(yàn)上的常規(guī)體系,如普通金屬,即滿足上述量子化的對(duì)稱性要求。其后該工作計(jì)算了兩個(gè)具體的模型:普通金屬和外爾半金屬模型、以及普通金屬和超導(dǎo)體模型的反常位移。計(jì)算結(jié)果顯示反常位移的矢量場(chǎng)在界面動(dòng)量空間中會(huì)形成量子漩渦,直接證明反常位移環(huán)流具有量子化的特性,如圖2和圖3所示。此外計(jì)算也表明量子化環(huán)流的值取決于外爾點(diǎn)和超導(dǎo)體的拓?fù)潆姾伞?/p>
該工作表明,如果目標(biāo)區(qū)域具有非零的拓?fù)潆姾桑瑒t會(huì)導(dǎo)致非平庸的量子化的環(huán)路積分。而這也反過來表明,反常位移的環(huán)路積分可以用來探測(cè)目標(biāo)區(qū)域的拓?fù)湮镄浴hb于量子化的物理量在物理學(xué)中所具有的重要性,該工作將極大的促進(jìn)反常位移和新奇拓?fù)洳牧系难芯俊?/p>
該文章發(fā)表于物理學(xué)頂級(jí)期刊《Physical Review Letters》,作者為劉影、余智明(通訊作者)、肖聰和楊聲遠(yuǎn)(Ying Liu, Zhi-Ming Yu*, Cong Xiao, and Shengyuan A. Yang),Physical Review Letters 125, 076801 (2020)。 文章鏈接:https://doi.org/10.1103/ PhysRevLett.125.076801
分享到:
